& copy Copyright StatSoft, Inc., 1984-2011
Поиск в руководстве по статистике Интернета
Основные понятия статистики Обзор основных понятий статистики. Вначале будут обсуждаться необходимые статистические концепции, которые составляют основу для лучшего понимания принципов работы в каждой области анализа статистических данных. Темы, обсуждаемые здесь, иллюстрируют основные идеи большинства статистических процедур и, как показали исследования, они представляют собой минимум, необходимый для понимания количественного характера окружающей нас реальности (Nisbett et al., 1987). Из-за нехватки места мы сосредоточимся в основном на функциональных аспектах обсуждаемых идей, и презентация будет очень короткой. Более подробную информацию о каждой из обсуждаемых тем можно найти в разделе «Введение и примеры» данного описания и в руководствах по статистике. Рекомендуемые учебники для начинающих: Kachigan (1986) и Runyon and Haber (1976); Те, кто заинтересован в более углубленных дискуссиях об основах теории и принципах, лежащих в основе статистики, относятся к классическим книгам: Хейс (1988) и Кендалл и Стюарт (1979).Каковы эти переменные? Переменные - это величины, которые мы измеряем, контролируем или определяем каким образом в ходе исследования. Переменные могут иметь разные свойства, особенно из-за их роли, как в нашем исследовании, а также из-за типа меры, которая может быть применена к ним.
Корреляционные исследования и экспериментальные исследования. Большинство эмпирических исследований можно классифицировать по одной из двух категорий: в корреляционном исследовании (наблюдательном) исследователь не (или, по крайней мере, не пытается влиять) на любые переменные, регистрируя только их и наблюдая отношения (корреляции) между некоторыми подмножествами переменных, например, между кровяное давление и уровень холестерина. В экспериментальных исследованиях исследователь определяет значения некоторых переменных и измеряет значения других переменных при заданных настройках. Например, исследователь может установить три уровня содержания алюминия в сплаве и измерить магнитные свойства сплава для каждого из этих уровней. Во время анализа данных, полученных в результате экспериментального исследования, также происходит расчет корреляции между переменными, в частности между измеряемыми переменными и теми, значения которых определяются из игры. Однако данные экспериментального исследования чаще всего дают более качественную информацию, чем данные корреляционных исследований. В частности, помните, что только экспериментальные тесты типа могут эффективно идентифицировать причинно-следственную связь между переменными. Если, например, мы обнаружим, что если мы изменим значение переменной A, то значение переменной B изменится, то мы можем заключить, что переменная A влияет на переменную B. Данные корреляционных исследований могут интерпретироваться только в причинно-следственной связи с учетом определенных теорий, но никогда не позволяют окончательно доказать существование причинно-следственной связи.
Зависимые переменные и независимые переменные. Мы называем переменные "spord", которые стоит изменить, а зависимые переменные только измеряются. Это различие кажется многим людям терминологически вводящим в заблуждение, потому что, как говорят студенты, все переменные зависят от того, что. Тот, кто однажды привыкнет к такому разбавлению, для этого становится незаменимым. Термины зависимость и независимость применяются главным образом в экспериментальных типовых исследованиях, в которых мы определяем значения определенных переменных в игре, и в этом смысле эти переменные не зависят от моделей поведения, намерений и т. Д. Особенностей объектов. Мы ожидаем, что значение зависимых переменных будет зависеть от значения независимых переменных. В некоторой степени противоречат характеру этого различия термины «независимые переменные» и «зависимые переменные». они могут также использоваться в наблюдательных исследованиях, где значение независимых переменных не определено, а только назначает объекты определенным экспериментальным группам на основе их характеристик. Если, например, в определенном эксперименте мужчин по сравнению с женщинами по количеству лейкоцитов, то Pe можно назвать независимой переменной, а количество белых линий (LBC) может варьироваться.
Измерительные весы. Переменные различаются с точки зрения того, насколько хорошо они могут быть измерены, то есть сколько измеряемой информации может быть получено во время их измерения. Разумеется, вышеприведенное утверждение следует рассматривать в свете того факта, что каждое измерение выполняется с ошибкой, которая ограничивает объем информации, доступной во время измерения. Другим фактором, определяющим объем информации, который может быть предоставлен данной переменной, является тип шкалы измерения. В этом отношении переменные делятся на: (а) номинальный, (б) порядок, (в) прерывание, (г) частное.
- Номинальные переменные допускают только качественную классификацию. Это означает, что они могут быть измерены только при завершении отдельных объектов (отдельных лиц, отдельных лиц и т. Д.) В одну из отдельных категорий, но эти категории не могут быть количественно измерены, и мы не можем ранжировать их в соответствии с рангом. Например, с точки зрения переменной A, мы можем только сказать, что два человека различны (например, с точки зрения расы), но мы не можем сказать, какой из них был описан A в большей степени. Типичными примерами номинальных переменных являются pe, раса, цвет, город и т. Д.
- Порядковые переменные позволяют ранжировать (устанавливать в определенном порядке) элементы, которые мы измеряем, в том смысле, что элемент ранга имеет признаки, представленные измеряемой переменной, в большей степени, но это еще нельзя сказать, насколько больше. Типичным примером переменной порядка является социально-экономический статус семей. Например, мы знаем, что статус выше среднего выше среднего, но мы не можем сказать, что он, скажем, на 18% выше. Действительно, серьезность, обсуждаемая здесь между номинальными шкалами, порядками и интервалами, является хорошим примером переменной порядка. Можно сказать, что номинальное измерение дает меньше информации, чем порядковое измерение, но мы не можем сказать, насколько меньше или равно сопоставимой разнице между шкалой порядков и интервалами.
- Интервальные переменные позволяют не только последовательно (ранжировать) измеряемые элементы, но и измерять различия в размере между ними. Например, температура, измеренная в градусах Цельсия, является переменным интервалом. Можно сказать, что температура на 40 градусов выше, чем температура на 30 градусов, и что повышение температуры с 20 до 40 градусов в два раза выше, чем с 30 до 40 градусов.
- Факторные переменные аналогичны межвалентным переменным, но, помимо всех особенностей прерывистой шкалы, они характеризуются абсолютной точкой ноль шкалы, что делает его действительным для переменных: х в два раза больше, чем у. Типичными примерами соотношений являются пространственные шкалы и время. Также шкала измерения температуры Кельвина является частной шкалой. Мы можем добиться успеха, и 200 градусов Кельвина - это температура, в два раза превышающая 100 градусов Кельвина. Интервальные весы не имеют этой функции. Следует отметить, что в большинстве статистических процедур не существует разрыва между диапазонами шкал и частными.
Отношения (отношения) между переменными. Независимо от того, какого типа две или более переменных находятся в отношении, если значения этих переменных в измеряемом образце распределены определенным, систематическим образом. Другими словами, переменные остаются в отношении, если их соответствующие значения зависят друг от друга. Например, Pe и LBC могут считаться находящимися в отношениях, если у большинства мужчин высокий LBC, а у большинства женщин низкий LBC (или наоборот). Увеличение связано с Телом, потому что обычно более высокие люди более важны. IQ (коэффициент интеллекта) связан с количеством ошибок в тэте, если люди с более высоким IQ запрашивают меньше ошибок и т. Д.
Почему зависимости (отношения) между переменными важны. Поиск связи между переменными является, вообще говоря, основной целью любого научного исследования. Философия науки учит нас, что нет другого способа выразить смысл, кроме как через отношения между определенными категориями количества или качества. В обоих случаях это сводится к обнаружению отношений между переменными. В корреляционных исследованиях измерение таких отношений происходит самым простым способом. Однако следует подчеркнуть, что экспериментальные типовые испытания не отличаются в этом отношении. Например, эксперимент, включающий сравнение LBC у женщин и мужчин, может быть определен как измерение корреляции между двумя переменными Pe и LBC. Статистика - это не что иное, как обучение, которое помогает нам оценить взаимосвязь между переменными. По правде говоря, сотни процедур, описанных в этом руководстве, можно интерпретировать с точки зрения оценки взаимосвязи между различными переменными.
Две основные особенности каждого отношения между переменными. Формально каждое отношение (зависимость) между переменными может характеризоваться двумя свойствами: (a) si (или «размер») и (b) достоверность (или «истинность») этого отношения.
- Сиа («великие») отношения (отношения) легче понять, чем доверие (существенное). Если, например, в измеренной выборке у каждого мужчины LBC выше, чем у любой женщины, мы можем сказать, что соотношение между двумя переменными (Pe и LBC) велико в измеренной выборке. Другими словами, одна переменная может быть предсказана на основе второго измерения (по крайней мере, в нашей выборке).
- Достоверность («правда») гораздо менее очевидна, но она чрезвычайно важна. Это относится к репрезентативности результатов, полученных на основе выборки по отношению ко всей изученной популяции. Он сообщает нам, какова вероятность того, что аналогичное (как указано в выборке, измеренной в настоящее время) будет измерено, если эксперимент будет повторен на других образцах, взятых из той же популяции. Давайте помнить, что исследователь никогда не ограничивает свой интерес к проверенному образцу, но на самом деле ему нужно только предоставить ему информацию обо всей изученной популяции. Если исследование проводится в соответствии с определенными правилами, которые будут обсуждаться позже, то достоверность измеренного отношения в образце можно количественно определить в виде определенного числа (технически называемый уровень значимости или уровень α, см. В следующем абзаце).
Что такое уровень значимости (уровень значимости α). Прежде всего, следует знать разницу между уровнем значимости α, который определяется, и статистической значимостью, то есть значением p, которое рассчитывается. Статистическая значимость результата представляет собой вероятность того, что наблюдаемые связи (например, между переменными) или различия (например, между средними значениями) в выборке появились чисто случайно (в случае случайности), если предположить, что в популяции, из которой была взята выборка, или различий не существует. Менее технически мы можем сказать, что статистическая значимость результата называется мерой (чем меньше истинная величина, тем выше) степень, до которой он верен (в смысле его представителя для всей изучаемой популяции). С технической точки зрения, именно значение р стоит уменьшения коэффициента достоверности результата (см. Brownlee, 1960). Чем выше значение p, тем меньше мы можем быть уверены, что соотношение, наблюдаемое в выборке, является надежным индикатором взаимосвязи между измеренными величинами во всей совокупности, которая нам интересна. С другой стороны, уровень значимости α равен допустимой вероятности ошибки, что мы принимаем результат как истинный, то есть представитель населения. Например, уровень 0,05 (т. Е. 1/20) означает, что мы допускаем вероятность 5% того факта, что обнаружение в выборочном тесте будет считаться днем события. Другими словами, предполагая, что такие отношения не встречаются в популяции, и мы будем повторять опыт один за другим в длинной гонке, мы можем ожидать, что в каждом двадцатом эксперименте измеренные отношения будут достаточно сильными, и мы считаем, что это указывает на невозможное предположение по поводу отсутствия отношений у населения. (Следует отметить, что это еще одно утверждение, что мы можем ожидать 5% или 95% повторяемости результатов при наличии взаимосвязи между переменными. Если существует взаимосвязь между переменными в совокупности, то вероятность повторяемости результатов и достоверность найденной взаимосвязи связана с статистическая сила тест. Смотрите также Анализ мощности теста ). Во многих областях уровень значимости 0,05 принимается как предел допустимого уровня ошибки.
Как он определит, действительно ли результат важен? Всегда произвольно решать, какой уровень серьезности мы считаем материальным. Это означает, что выбор уровня существенности, выше которого результат будет отклонен как несущественный, является договорным выбором. На практике это означает, что окончательное решение в этом отношении зависит от многих факторов: будет ли результат предсказан априори, получен ли он задним числом (после факта) в результате многих анализов и сравнений, проведенных с данным набором данных, от силы накопленного Сертификаты, подтверждающие это и от традиций, которые преобладают в данной области исследований. Во многих областях это считается типичным предельным значением значимости α = 0,05. Если значение p, полученное в образце, ниже этого значения, результат оценивается как статистически значимый. Памита, однако, следует отметить, что это значение несет в себе много ошибок (5%). Значимые результаты при α = 0,01 обычно считаются статистически значимыми, поскольку значимые результаты на уровне α = 0,005 или α = 0,001 называются высоко значимыми. Напомним, однако, что такие классификации - не что иное, как обычные соглашения, основанные на опыте исследований.
Значительно статистический и количество проведенных анализов. Памите нужно сказать, что чем больше анализов мы проводим с данным набором данных, тем больше число результатов может случайно превысить установленный уровень релевантности. Если, например, мы посчитаем коэффициенты корреляции между десятью переменными (45 факторов корреляции), мы можем ожидать, что случайно две из них (т.е. одна на каждые 20) будут значимыми на уровне α = 0,05, даже если значения являются переменными Они были полностью случайными, и между этими переменными в общей популяции нет корреляции. Некоторые статистические процедуры, в которых вы имеете дело со многими отклонениями (и, следовательно, с большей вероятностью возникновения таких ошибок), предусматривают специальные исправления или корректировки в зависимости от пористости. Большинство основных статистических методов (и, в частности, методов интеллектуального анализа данных) не предлагают никаких решений, позволяющих избежать подобных ситуаций. Это обстоятельство предъявляет исследователю особые требования к осторожности при оценке неожиданных результатов исследования. Многие примеры в этом руководстве дают советы о том, как бороться с такими случаями. Инструменты статистики также рекомендуются в качестве источника знаний в этом отношении.
Это надежные отношения между переменными. Ранее мы уже говорили, что sia и доверие - это две разные характеристики отношений между переменными. Они не одинаково независимы друг от друга. В основном, рассматривая это, вы можете сказать, что в выборке из определенного числа, чем больше зависимость между переменными, тем важнее это отношение (см. Следующий абзац).
Почему более сильные отношения между переменными важнее? Если мы ожидаем, что между интересующими нас переменными нет никакой связи, наиболее вероятным результатом статистического обследования в выборке также будет отсутствие такой связи. Исходя из этого, легко сделать вывод, что чем сильнее была измерена связь между переменными в выборке, тем меньше вероятность того, что в общей популяции таких связей нет. Как вы можете видеть, отношения и значение отношений между переменными связаны и могут быть значительно рассчитаны на основе значения отношений и наоборот. Это утверждение, однако, верно только в отношении выборки фиксированного размера. Отношение (zaleno) с заданной силой может оказаться очень важным или совершенно неактуальным в зависимости от размера образца (см. Следующий параграф).
Почему значимость отношений между переменными зависит от размера выборки. Если мы имеем дело с количеством наблюдений, то существует также небольшое количество всех возможных комбинаций различных значений отдельных переменных, и, следовательно, вероятность того, что измерение произойдет случайно, указывает на то, что сильная связь относительно велика. Мы разработаем следующий пример. Если нас интересуют две переменные (Peñman / woman и LBC - high / low) и у нас в выборке только четыре объекта (две женщины и два мужчины), то вероятность того, что мы найдем 100% -ную связь между переменными по чисто случайным причинам. 1/8. Вероятно, и у обеих женщин низкий LBC, и у обоих мужчин высокий LBC (или для возмездия), эквивалентный один смей. Давайте теперь рассмотрим, что было бы шансом в выборке из 100 объектов. Счет указывает, что этот шанс практически нулевой в то время. Давайте проанализируем более общий пример. Мы представляем теоретическую популяцию, в которой среднее значение LBC для мужчин и женщин одинаково. Очевидно, что если мы начнем последовательный эксперимент, включающий отрисовку пар выборок фиксированного размера (выборка мужского и женского пола) и вычисление среднего значения LBC в каждой паре выборок, большинство результатов будет близко к 0. Однако время от времени случайная нарисованная пара образец даст результат, который будет значительно отличаться от нуля. Как часто вы можете ожидать такого результата? Чем меньше количество выборок, тем чаще результат будет больше, что свидетельствует о существовании взаимосвязи, которой не существует в общей популяции.
Пример: соотношение количества рождений девочек и мальчиков. Я отметил следующий пример из исследования статистического вывода (Nisbett et al., 1987). Мы записываем количество рождений девочек и мальчиков в двух больницах. В одном из них 120 детей рождаются каждый день, а в течение вторых 12 месяцев в среднем в каждой из больниц рождается одинаковое количество мальчиков (отношение числа рождений составляет 50/50). Однажды в одной из больниц было рождено вдвое больше девочек, чем мальчиков. В какой из больниц это произойдет? Ответ очевиден для статистики, но, как показывают исследования, он не так очевиден для неспециалистов. Вероятность такой ситуации несравненно выше в меньшей из больниц, вероятность того, что 120 детей, родившихся в более крупной больнице, будет вдвое больше, чем число девочек, практически равна нулю. Это связано с тем, что вероятность случайного отклонения с определенной пропорцией по отношению к среднему значению уменьшается с увеличением количества выборок.
Почему небольшие эффекты можно обнаружить только при больших размерах выборки? Приведенные выше примеры (см. Предыдущий абзац) показывают, что если отношение между переменными объективно (то есть в общей популяции) может быть значительным, то невозможно обнаружить такую зависимость иначе, чем в случае выборок большого числа. Даже если наша выборка является совершенно репрезентативной, результат не будет статистически значимым, если выборка мала. Аналогично, в случае, когда зависимость объективно (в общем населении) очень сильная, это можно доказать, даже если выборка невелика. Пусть это будет проиллюстрировано следующим дополнительным примером. Если мы бросим немного асимметричные монеты (скажем, с соотношением 40% к 60% или хвостам), десяти бросков будет недостаточно, чтобы убедить кого-либо в его асимметрии (даже если в результате опыта мы получим совершенно репрезентативный результат: от 4 до 6). Возникает вопрос: слишком мало десяти бросков, чтобы что-то доказать о нашей монете? Ответ таков: если эффект, который мы хотим доказать, очень сильный, то десяти бросков может быть достаточно! Например, предположим, что монета, о которой мы говорим, настолько асимметрична, и независимо от того, как вы ее разыгрываете, всегда оставляет орла. Если какие-либо скептики демонстрируют десять бросков каждый раз, когда они заканчивают бросать ора, то больше всего это будет убедительным аргументом, что наши монеты не правы. Другими словами, этот результат можно рассматривать как убедительное свидетельство того, что при теоретической совокупности бесконечного числа проекций он часто выпадает из головы. Так что, если отношения крепкие, это будет важно даже в небольшой выборке.
Можно ли считать отсутствие отношений значительным результатом? Чем меньше взаимосвязь между переменными, тем больше необходим большой образец, чтобы доказать это. Например, давайте попробуем представить, сколько проекций необходимо для асимметричного обнаружения монеты 0,000001%! Очевидно, что необходимое количество образцов увеличивается с уменьшением тестируемого эффекта. Когда большой эффект достигает нуля, тогда большое количество образцов, необходимых для его обнаружения, должно увеличиться до нового. Это означает, что если связь между переменными пренебрежимо мала, то многие выборки должны быть сопоставимы с численностью населения, что является огромным сюрпризом. Статистическая значимость представляет вероятность того, что аналогичный результат будет получен, если мы изучим всю популяцию. Другими словами, все, что можно продемонстрировать после изучения всего населения в целом, по определению необходимо на самом высоком уровне материальности. Это также относится к результату отсутствия изучаемых эффектов (отсутствие связи между переменными).
Как можно измерить соотношение между переменными? Статистики предложили множество мер для связи между переменными. Выбор того, какой из них в конкретном случае зависит от того, сколько переменных включено в расчет, каковы масштабы измерения, какова природа исследуемых отношений и т. Д. Однако почти все они основаны на принципе сравнения силы изученных отношений с максимально возможной зависимостью для переменных, какие измерения мы делаем. Используя профессиональный язык, нормальный способ сделать такую оценку состоит в том, чтобы изучить изменение (вариацию) в значении измеряемых переменных, а затем вычислить, какая общедоступная волатильность может быть отнесена к тому факту, что изменчивость является общей для двух или более изученных переменных. В менее технической терминологии это можно выразить так, что мы сравним то, что является общим для интересующих нас переменных, с тем, что было бы для них общим, если бы они были связаны друг с другом на сто процентов. И давайте просто отпустим простую иллюстрацию. Слухи о том, что в исследуемой нами выборке среднее значение LBC составляет 100 для мужчин и 102 для женщин. Можно сказать, что в среднем отклонение каждого значения, измеренного от общего среднего (101), включает компонент, связанный с pci; Этот элемент имеет большую величину 1. Это значение в некотором смысле представляет собой меру взаимосвязи между переменными Pe и LBC. Однако это плохая мера, потому что она не говорит нам, насколько обсуждаемый компонент относительно относительно общей волатильности значения LBC. Мы разработаем две крайние возможности:
- Если бы все значения LBC для мужчин были ровно 100, а для женщин 102, то все отклонения от общего среднего в нашей выборке можно было бы отнести к фактору pci. Можно сказать, что в нашей выборке pe прекрасно коррелирует с LBC, то есть 100% наблюдаемых различий между исследуемыми объектами можно отнести к pci.
- Если бы значения LBC находились в диапазоне 0-1000, то такая же разница (2) между средними значениями LBC для мужчин и женщин была бы настолько малой составляющей общей изменчивости этих значений, что можно было бы считать ее незначительной. Например, добавление одного дополнительного элемента в выборку может привести к полному развороту наблюдаемой тенденции. Хорошая мера взаимосвязи между переменными должна, следовательно, учитывать общую изменчивость выборки и оценивать взаимосвязь по тому, как часть этой общей вариации можно отнести к ее влиянию (объясняется влиянием этой взаимосвязи).
Общий общий пост большинства статистических тестов. Поскольку конечной целью большинства статистических тестов является оценка взаимосвязей между переменными, поэтому большинство этих тестов имеют общий пост, основанный на принципах, описанных в предыдущем абзаце. Опять же, используя профессиональную терминологию, они основаны на значении отношения определенного показателя общего отклонения представляющих интерес переменных к их общей (общей) изменчивости. Например, это может быть отношение этой части общей волатильности LBC, что можно объяснить влиянием фактора pci на общую волатильность LBC. Это соотношение обычно называют отношением вариаций, объясняемых общей волатильностью. Как часть статистической терминологии, понятие , которое поочередно объясняется , не означает, что исследователь понимает эту вариацию в концептуальном смысле. Мы используем его только для того, чтобы указать, что это общая вариация изучаемых признаков, то есть одна часть вариации одной переменной, что можно объяснить значениями второй переменной и наоборот.
Как оценить значение значимости. Слухи о том, что мы уже рассчитали отношения между двумя переменными (как описано выше). Сразу возникает вопрос: насколько важны эти отношения? Например, 40% объясненного отклонения достаточно, чтобы считать отношения существенными? Ответ: это зависит. Прежде всего, это зависит от количества образцов. Как мы говорим ранее, на основе очень большой выборки даже очень слабая зависимость может считаться значимой, в то время как небольшие выборки не позволяют оценить достоверность даже очень сильных отношений. Существует необходимость иметь функцию, которая выражала бы взаимосвязь между значимостью взаимосвязи между переменными в зависимости от количества выборок. Такая функция ответила бы на вопрос: насколько вероятно получить наблюдаемую (или большую) зависимость в выборке данного размера, предполагая, что эта связь вообще не существует в общей популяции? Другими словами, эта функция дает значение вероятности ошибки, состоящей в том, чтобы отвергнуть гипотезу о том, что исследуемые нами отношения не встречаются в общей популяции (в то время как мы предполагаем, что реальность присутствует). Эта гипотеза (отсутствие зависимости в общей популяции) называется гипотезой нулевой статистики. Было бы идеальным состоянием, если бы рассматриваемая функция была линейной функцией. К сожалению, ее пост во многих случаях более сложен и отличается. К счастью, однако, в большинстве случаев мы знаем его форму и можем использовать его для расчета уровня значимости для разного количества образцов. Большинство из этих функций связаны с общим типом функций, известным как распределитель нормального распределения.
Почему нормальное распределение важно. Нормальное распределение важно, потому что во многих случаях оно в достаточной степени приближает функцию, описанную в предыдущем абзаце (более подробную информацию можно найти в части У всех тестовых статистик нормальное распределение? ). Распределение многих тестовых характеристик является нормальным распределением или может быть получено в результате преобразования нормального распределения. В этом смысле, с философской точки зрения, нормальное распределение представляет собой эмпирически подтвержденные «истины о сущности вещей», и его статус можно сравнить со статусом фундаментальных законов естествознания. Точная форма нормального распределения (характеристика «кривая колокола») определяется функцией, имеющей только два параметра: среднее значение и стандартное отклонение, когда нормальное распределение не является одним и только всем их семипараметрическим семейством.
Характерной особенностью нормального распределения является то, что 68% всех описанных случаев относятся к диапазону со средним значением ± 1 стандартного отклонения, а среднее значение интервала ± 2 стандартных отклонения охватывает 95% случаев. Другими словами, в нормальном распределении стандартизированные значения меньше -2 и больше +2 могут встречаться на частотах около 5% (стандартизованное значение рассчитывается путем вычитания его среднего значения из переменной и деления результата на стандартное отклонение). Значения вероятностей в нормальном распределении можно перенести с помощью калькулятора вероятностей в модуле « Базовая статистика ». Если, например, мы введем стандартизированное значение Rwn 4, то вероятность, рассчитанная программой STATISTICA, будет меньше 0,0001, потому что в нормальном распределении почти все наблюдения (более 99,99%) достигают диапазона среднего ± 4 стандартных отклонения. Следующая анимация показывает вероятности для других значений переменной с нормальным распределением.
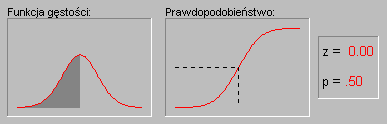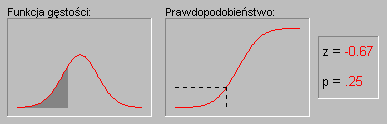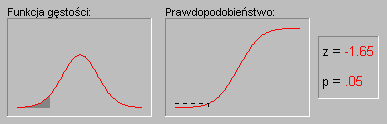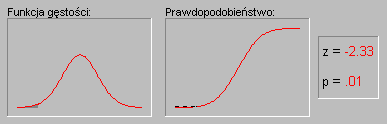
Иллюстрация применения нормального распределения в статистическом выводе (индукции). Давайте вспомним рассмотренный выше пример, в котором пары мужской и женской выборок были взяты из общей популяции, в которой среднее значение LBC для обоих полов было точно одинаковым. Хотя обычно результат такого эксперимента (одна пара образцов в эксперименте) будет основываться на отсутствии различий в средних значениях LBC в обоих образцах, время от времени в какой выборке результат может значительно отличаться от нуля. Как часто мы этого ожидаем? Если выборка достаточно велика, то результаты такого удара подчиняются нормальному распределению (основной принцип будет обсуждаться в следующем параграфе). Таким образом, мы знаем форму нормального распределения, мы можем точно рассчитать вероятность случайного получения результатов, при которых средние различия превышают любую игру заданное значение (отклоняется от гипотетического значения в популяции - равно 0 по любому размеру). Если рассчитанная таким образом вероятность настолько мала, что она не превышает заранее заданный уровень значимости, то исследователь должен учитывать, что полученный результат лучше описывает реальную ситуацию в общей популяции, чем нулевая гипотеза. Напомним, что нулевая гипотеза была сформулирована по чисто техническим причинам, в качестве ссылки на которую мы оцениваем результат нашего опыта. Мы отмечаем, что все вышеприведенные рассуждения основаны на предположении, что распределение этих отходов (распределение статистики теста из испытания) является нормальным. Это предположение будет обсуждаться в следующем параграфе.
У всех тестовых статистик нормальное распределение? Не все из них, но большинство из них либо напрямую связаны с нормальным распределением, либо связаны с ним, например: T , F или Хи-квадрат , Обычно такие тесты требуют, чтобы сами исследуемые переменные были нормальными. Мы называем это идеей нормальности. Многие переменные, фактически встречающиеся в экспериментах, имеют нормальное распределение, что является дополнительной причиной, по которой нормальное распределение играет такую большую роль в естественных науках. Проблема возникает, когда кто-то пытается применить тест на основе предположения о нормальности к переменным, которые не имеют нормального распределения (см. Тесты стандарта в описании модулей). Непараметрическая статистика или ANOVA / MANOVA ). В таких случаях у нас обычно есть два варианта: мы можем применять тесты, которые не требуют стандартизации (иначе известные как непараметрические или непараметрические тесты, см. Непараметрическая статистика); это обычно неудобно из-за силы таких тестов и их негибкой природы при формулировании заявок, или, тем не менее, мы можем быть использованы для обычных тестов, при условии, что у нас достаточно большая выборка. Последнее основано на чрезвычайно важном предложении, согласно которому тесты, основанные на нормальном распределении, имеют такое большое значение. Это говорит о том, что с увеличением количества выборок распределение тестовой статистики на основе среднего значения (Fisher, 1928a) переходит к нормальному распределению, независимо от распределения измеряемой нами переменной. Следующая анимация иллюстрирует это утверждение. Мы видим, что количество выборок увеличивается (выборки с номерами последовательно: 2,5,10,15 и 30) изменяют среднее распределение выборки для переменной с очень асимметричным (scony) распределением, которое отличается от нормального.
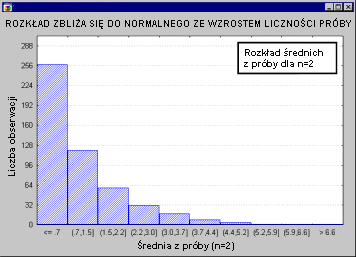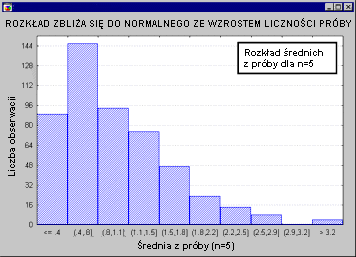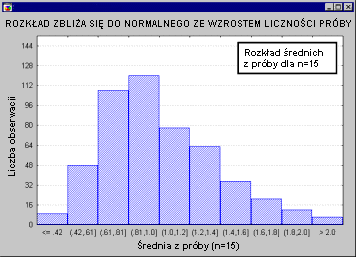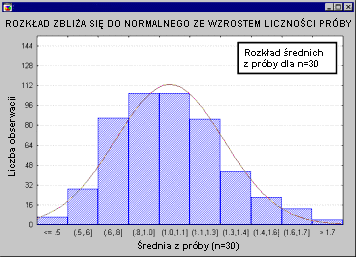
По мере увеличения количества выборок (для выборок, используемых для определения распределения статистики из выборки) распределение статистики из выборки становится все более нормальным. Отметим, что для n = 30 распределение «почти» полностью соответствует нормальному (как мы видим, скорректированное нормальное распределение очень близко к распределению статистики из испытания). Это утверждение называется центральной предельной теоремой (этот термин был впервые использован Пля, 1920, «Zentraler Grenzwertsatz»).
Скд, мы знаем о последствиях неспособности принять нормальность? Хотя многие из цитаделей, упомянутых ранее, могут быть изучены математическими методами, некоторые из них все еще не имеют таких доказательств и могут быть продемонстрированы только эмпирическим путем с использованием так называемого метода Монте-Карло. В эксперименте, проводимом этим методом, большое количество образцов генерируется с использованием компьютера. Эти образцы имеют свои собственные свойства из игры, а полученные из них результаты затем анализируются с использованием ряда различных тестов. Таким образом, можно эмпирически оценить типы и размеры ошибок, которые имеются, когда проанализированные данные не удовлетворяют определенным требованиям, необходимым для применения конкретных тестов. Методы Монте-Карло интенсивно использовались, чтобы исследовать влияние отсутствия стандартизации на поведение тестов на основе этого предположения. Общий вывод, который он делает из этих исследований, состоит в том, что последствия упорядочения предположения о нормальности не столь серьезны, как считалось ранее. Хотя этот вывод не должен побуждать кого-либо отказываться проверять достоверность своих исследований, он, безусловно, увеличивает популярность статистических тестов, применяемых к нормальному распределению во всех областях исследований.

& copy Copyright StatSoft, Inc., 1984-2011
STATISTICA является торговой маркой StatSoft, Inc.
Похожие
Компоненты низкой стоимости: основные средства или оборудование?Вопрос: Должны ли устройства, которые будут использоваться более года, быть постоянными и, следовательно, включаться в учет основных средств или в связи с покупной стоимостью до 3500 нетто, должны ли они быть оборудованием? Однако в тех случаях, когда первоначальная стоимость не превышает 1500 злотых нетто, они не должны включаться в учет основных средств, а также в реестр оборудования, и является ли вычитаемая из налогов стоимость на дату их ввода в действие? Транспортно-экспедиционные различия
Итак, короткий урок из словаря логистики Иногда наиболее распространенные понятия могут быть самыми трудными для расшифровки. В логистической отрасли , как и во многих других, существуют спорадические особенности и термины, которые могут вызвать значительные проблемы для потребителей, желающих воспользоваться этими услугами. В следующей статье мы попытаемся Как определить временные различия между балансовой и налоговой стоимостью основных средств?
Статья эксперта PKF (Эвелина Возняк, координатор финансовых и бухгалтерских проектов PKF) была опубликована в газете Rzeczpospolita 16 июня 2014 года. Причины различий в балансовой и налоговой оценке Субъекты, которые обязаны вести бухгалтерские книги в соответствии с Законом о бухгалтерском учете (в дальнейшем именуемые «анионами»), применяют для целей бухгалтерского учета принципы и методы оценки активов и обязательств, включенных в него. В определенных ситуациях Где взять биржевую информацию и информацию от компаний?
... основные данные от польских акционерных обществ, котирующихся на Варшавской фондовой бирже. Абсолютно необходимо для всех тех, кто инвестирует на польском рынке акций и облигаций. Stockwatch.pl Фондовая биржа Прежде всего, он содержит целый набор готовых индикаторов, описывающих каждую компанию с польской фондовой биржи. Доступ к большому Каковы эти переменные?
Как он определит, действительно ли результат важен?
Почему более сильные отношения между переменными важнее?
В какой из больниц это произойдет?
Почему небольшие эффекты можно обнаружить только при больших размерах выборки?
Возникает вопрос: слишком мало десяти бросков, чтобы что-то доказать о нашей монете?
Можно ли считать отсутствие отношений значительным результатом?
Как можно измерить соотношение между переменными?
Сразу возникает вопрос: насколько важны эти отношения?
Например, 40% объясненного отклонения достаточно, чтобы считать отношения существенными?